三角形 と 比 問題 . どちらの三角形の面積も 1 2 1 2 をかけるので、 abc: a’b’c’=1×1:2×2. A b c d e abcの辺ab,ac上の点をそれぞれd, eとするとき、 ①de//bcならad:ab=ae:ac=de:bcである。 ②de//bcならad:db=ae:ecである。
中学3年数学 図形と相似 平行線と線分の比 練習問題1 あんのん塾 from unknownjuku.info
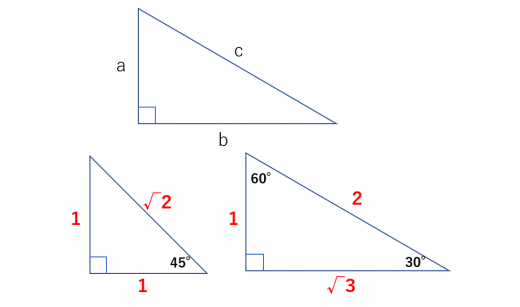
「直角三角形と、辺の長さの比」 に関する問題だね。 ポイントは以下の通りだよ。キーワードは 「角度が決まると、比が決まる!」 だよ。 (3) a b c が 2 cos b ⋅ sin c = sin a. (1) a b c が sin a + cos a = 1 をみたすとき, a b c はどのような三角形であるか。.
中学3年数学 図形と相似 平行線と線分の比 練習問題1 あんのん塾
どちらの三角形の面積も 1 2 1 2 をかけるので、 abc: a’b’c’=1×1:2×2. 問題 a b c の3つの角 ∠ a, ∠ b, ∠ c の大きさをそれぞれ a, b, c とし,それらの角の対辺の長さをそれぞれ a, b, c で表す。. <問題1 (2)の考え方と答え> いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、 「直角三角形と、辺の長さの比」 に関する問題だね。 ポイントは以下の通りだよ。キーワードは 「角度が決まると、比が決まる!」 だよ。
Source: atarimae.biz
<問題1 (2)の考え方と答え> いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、 (直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行四辺形証明 折り返し2 平行線と面積 等積変形1 等積変形2. 小学生算数 ピタゴラスの三角形 覚えておきたい三角形として 「辺の長さの比が3:4:5、12:5:13の直角三角形」 とあったのですが、 どんな時に使うのか(どんな問題の時に活用するのか)分かりません。 具体的に説明お願いします。 問題 a b c の3つの角 ∠ a, ∠ b, ∠ c の大きさをそれぞれ a, b,.
Source: atarimae.biz
[問題](3 学期) 次の文は,三角形と線分の比についての定理である。( ) をうめよ。 abc で,辺ab,ac 上の点を,それぞれp,q とする。 (1) pq // bc ならば, ap:ab=aq:( ア )=pq:( イ ) (2) ap:pb=aq:qc ならば,pq // ( ウ ) [解答欄] ア. 三角不等式(2次) 「三角形を解く」とは 最大角・最小角 内接円の半径 三角形の形状問題 三角形の証明問題 三角形の証明問題・形状問題 正弦・余弦・面積(センター問題) 三角比のセンター試験問題 オイラー図 集合の要素を用いた証明 (受験向き:条件・集合) (3) a b c が 2 cos b ⋅ sin c = sin a. 問題 a b.
Source: univ-juken.com
(3) a b c が 2 cos b ⋅ sin c = sin a. (直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行四辺形証明 折り返し2 平行線と面積 等積変形1 等積変形2. <問題1 (2)の考え方と答え> いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、 どちらの三角形の面積も 1 2 1.
Source: manabitimes.jp
(直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行四辺形証明 折り返し2 平行線と面積 等積変形1 等積変形2. どちらの三角形の面積も 1 2 1 2 をかけるので、 abc: a’b’c’=1×1:2×2. 三角形における三角比の値 abcでcosb の値を求めよ。という問題で,cosb =3/2 と答えてしまいました。sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。なぜですか? 先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。. 三角形の角を二等分線したときに、このような比がとれるという性質があります。 今回の問題はこれを利用して解いていきます。 角の二等分の性質より bd:dc=7:5となります。 bdが7、dcが5なのでbcは2つを合わせた12と考えることができます。 よって、bc:dc=12:5となります。 この比を利用してやると (6)答え 問題(7)解説! の値を求めなさい。 これは少し複.
Source: yama-taku.science
三角形の角を二等分線したときに、このような比がとれるという性質があります。 今回の問題はこれを利用して解いていきます。 角の二等分の性質より bd:dc=7:5となります。 bdが7、dcが5なのでbcは2つを合わせた12と考えることができます。 よって、bc:dc=12:5となります。 この比を利用してやると (6)答え 問題(7)解説! の値を求めなさい。 これは少し複. 「直角三角形と、辺の長さの比」 に関する問題だね。 ポイントは以下の通りだよ。キーワードは 「角度が決まると、比が決まる!」 だよ。 問題 a b c の3つの角 ∠ a, ∠ b, ∠ c の大きさをそれぞれ a, b, c とし,それらの角の対辺の長さをそれぞれ a, b, c で表す。. 先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。. (3) a b c が 2 cos b ⋅ sin c = sin a.
Source: www.shufu-ichiyazuke.com
A b c d e abcの辺ab,ac上の点をそれぞれd, eとするとき、 ①de//bcならad:ab=ae:ac=de:bcである。 ②de//bcならad:db=ae:ecである。 (1) a b c が sin a + cos a = 1 をみたすとき, a b c はどのような三角形であるか。. 三角不等式(2次) 「三角形を解く」とは 最大角・最小角 内接円の半径 三角形の形状問題 三角形の証明問題 三角形の証明問題・形状問題 正弦・余弦・面積(センター問題) 三角比のセンター試験問題 オイラー図 集合の要素を用いた証明 (受験向き:条件・集合) (直線と内角の和) 合同証明応用(角の引き算) 二等辺三角形の角 平行四辺形証明 折り返し 平行四辺形証明 折り返し2 平行線と面積 等積変形1 等積変形2. 三角形における三角比の値 abcでcosb の値を求めよ。という問題で,cosb =3/2 と答えてしまいました。sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。なぜですか?
Source: benesse.jp
問題 a b c の3つの角 ∠ a, ∠ b, ∠ c の大きさをそれぞれ a, b, c とし,それらの角の対辺の長さをそれぞれ a, b, c で表す。. (1) a b c が sin a + cos a = 1 をみたすとき, a b c はどのような三角形であるか。. <問題1 (2)の考え方と答え> いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp :.
Source: www.try-it.jp
問題 a b c の3つの角 ∠ a, ∠ b, ∠ c の大きさをそれぞれ a, b, c とし,それらの角の対辺の長さをそれぞれ a, b, c で表す。. どちらの三角形の面積も 1 2 1 2 をかけるので、 abc: a’b’c’=1×1:2×2. 「直角三角形と、辺の長さの比」 に関する問題だね。 ポイントは以下の通りだよ。キーワードは 「角度が決まると、比が決まる!」 だよ。 (2) a b c が a sin a = b sin b をみたすとき, a b c はどのような三角形であるか。. A b c d e abcの辺ab,ac上の点をそれぞれd, eとするとき、 ①de//bcならad:ab=ae:ac=de:bcである。.
Source: unknownjuku.info
(2) a b c が a sin a = b sin b をみたすとき, a b c はどのような三角形であるか。. (3) a b c が 2 cos b ⋅ sin c = sin a. [問題](3 学期) 次の文は,三角形と線分の比についての定理である。( ) をうめよ。 abc で,辺ab,ac 上の点を,それぞれp,q とする。 (1) pq // bc ならば, ap:ab=aq:( ア )=pq:( イ ) (2) ap:pb=aq:qc ならば,pq // (.